機能創造理工学II　　　　　　　<<<戻る

2010年 担当、後藤貴行、春学期・水曜一限・3-348

これまで学んだニュートン運動方程式を使えば、微分方程式（＝数学）さえ出来れば、ロボットでもスペースシャトルでも回転寿司の回る台でも、日常におけるすべての運動の問題が解けます。しかし、現代社会においてニュートン力学を適用出来ないケースが三つ存在します。それは、

1. 粒子の数がとてつもなく多い場合
2. 粒子がとてつもなく小さい場合

3. 粒子の速度がとてつもなく速い場合

の場合です。現代社会を支える、金属、半導体の中の電子は1と2にあてはまりますし、光通信やレーザーに登場する光子は3です。光を操作したり検知するデバイスを作るには1-3の全てが必要です。それから、未だに殆ど解明されていない現象の代表例として、摩擦があります。表面がつるつるしていれば良いかと言うとそうではなく、原子レベルで平坦な金属を貼り合わせると滑るどころかくっついて離れません。これを理解するのにも1と2が必要です。実は、1と2を理解するための科目は、「統計力学」と、「量子力学」と言って、これから先、どんどん習って行くわけですが、その準備をするための講義が機能創造理工学IIです。

※ 3は「相対論」です。残念ながら、本講義では深く取り扱うことはしません。

1. 第一回、　変分法　「積分の中身の関数をいろいろ変えて、積分値が最小になるようにするのが変分法。二点間を最短距離で結ぶ関数は直線。」
2. 第二回、　最小作用の原理　「ラグランジアンL＝E_運動−E_{ポテンシャル}　を時間で積分したものを作用積分と言う。現実の運動では作用積分が最小になる」
3. 第三回、　オイラー・ラグランジュ方程式　「ラグランジアンの満たす方程式」
4. 第四回、　エネルギーや運動量の保存則はどこから来るか？
5. 第五回、　角運動量の保存則はどこから来るか？　神様は左利き？
6. 第六回、　力学的相似（スケーリング）。ケプラーの第三法則があっという間に、、。
7. 第七回、　（ノートは前回の続き）一次元周期運動、惑星の運動を横から眺めると、、。
8. 第八回、　バネでつながれた多数の粒子の運動。座標変換とラグランジアン、基準座標
9. 第九回、　（ノートは前回の続き）バネでつながれた∞個の粒子の運動、弦を伝わる縦波、重ね合わせの原理が成り立つときと成り立たないとき
10. 第10回、　ラグランジアンからハミルトニアンへ（ルジャンドル変換）、熱力学変数U, F, H, Gもルジャンドル変換（ラッキーセブンの公式）
11. 第11回、　ハミルトニアンと正準方程式、正準変換（例示のみ）
12. 第12回、　（ノートは前回の続き）ハミルトニアンと正準方程式、正準変換（例示のみ）
13. 第13回、　位相空間、位相空間の体積は不変（Liouvilleの定理)、有界な位相空間ではいつか戻る（ポワンカレの再帰定理）、等重率の原理、統計力学への道
14. 第14回、  断熱不変量、作用変数、量子力学への道

15. 試験（略解）、二次元極座標変換(L, H)、重力場中の二質点による調和振動子の重心座標、ベクトルポテンシャルと磁場によるハミルトニアン　
    
    パイ中間子は、原子核の中で陽子と陽子をくっつける働きをします。パイ中間子は自転していません（自転の角運動量＝０）。
    パイ中間子を核の外へ取り出すと、あっという間に崩壊して、ニュートリノとミュー粒子の二つになってしまいます。
    左のミュー粒子自転の方向が、進行方向に対して「左巻き」になっていることを覚えておきましょう。
     
    
    
    
    
    
    
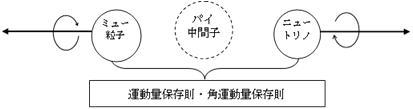
    上の図で空間反転させてみましょう。角運動量の和は０なのですから、

    

    となります。今度はミュー粒子の自転の方向は運動量に対して「右巻き」になります。しかし、実際にパイ中間子を崩壊させると、
    出てくるミュー粒子は全て「左巻き」なのです。つまり、鏡に映った世界（正確には空間反転させた世界）は、実現しないのです。
    この事実が発見された当初は「神様は左利きだった！？」とさえ言われていました。これは「自然界における対称性の破れ」の一つです。
    数年前までは、電荷の符号も同時に入れ替えると対称的になると言われていましたが、最近、時間の進みも反対にしてやらないとダメ
    なことが小林・益川の両先生によって明らかになり、ノーベル賞へと繋がったというわけです。

    【余談】また、後藤研で研究しているミューエスアール（μSR）という実験は、このミュー粒子を用いて、超伝導体や磁性体の中のようすを
    ミクロに調べますが、それが可能なのは、ミュー粒子の角運動量が進行方向にいつも揃っている（＝対称性が破れている）おかげです。

【2009年度の本講義のページへ】

もっと前の過去問（解析力学という科目をwebページ内で検索して、その試験問題を見て下さい）

大学院入試にもいくつか、解析力学から出題されています。

<<<戻る