ZN formulas
Fortran code for the Zhu-Nakamura formulas [Original paper]
The attached routines written in Fortan are used for ZN-TSH computation. The main subroutine for the ZN formulas is "hop.f" at the top of the hierarchy structure shown below. This routine returns the hopping probability between the two potential energy surfaces and the corresponding phase induced by the transition.
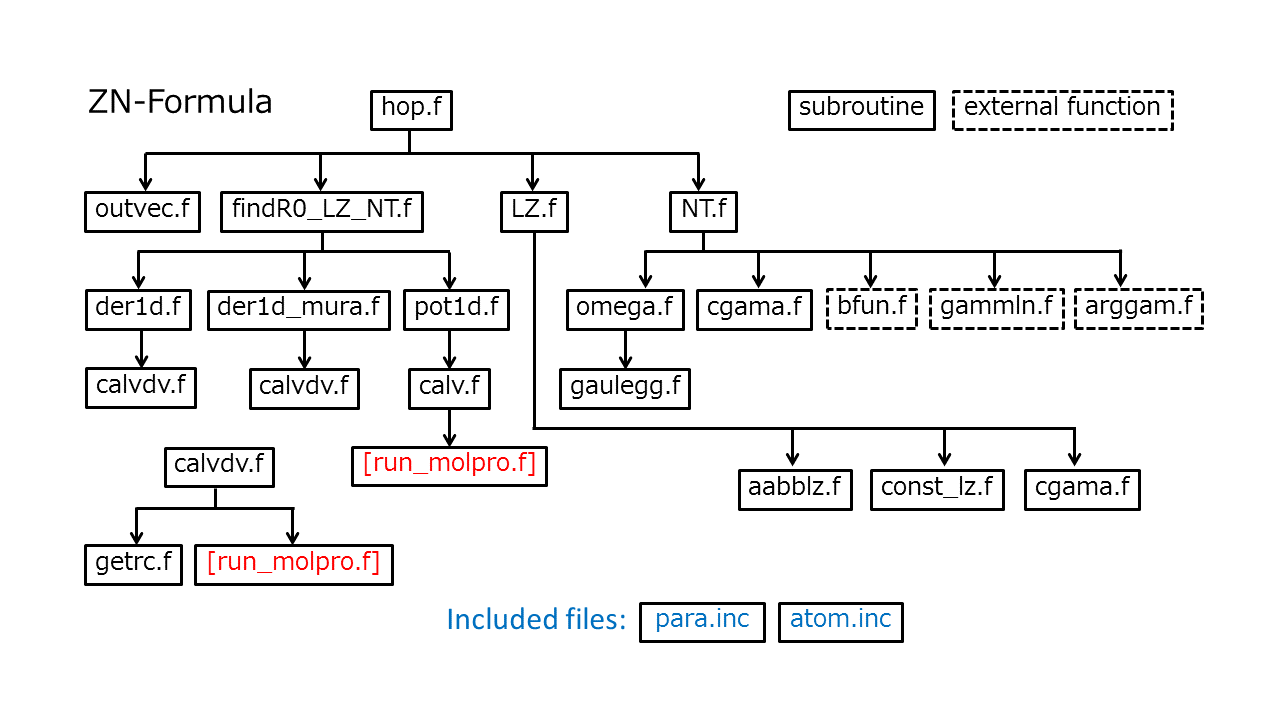
Fig. 1 shows all the routines and their hierarchy. The "run_molpro.f" in red represents the routine that should be supplied by the user. Here, it is assumed that the Molpro (version 2012)[Molpro12] is employed for the on-the-fly ab initio computation. Executing "call system("molpro input.com")" in Fortran code, the user can run the ab initio program. If the user-supply main program reads the output file and gives all data in the subroutine "hop.f", the code starts to compute the hopping probability. The interfaces of the main subroutine (hop.f) and the user-supply subroutine run_molpro.f are shown in the sections A and B below.
Some of the main subroutines are explained below with the information of the corresponding section and page number in the text.
- findR0_LZ_NT.f finds \(R_0\) as shown in Fig. 1 in Section 2 on page 6.
- LZ.f computes the quantities in Sections 2.1.1 and 2.2.1 on pages 6-8 and 10-11.
- the transition probability, \(p_{\rm ZN}\) [Eqs.(2.11) and (2.41)]
- the phases, \(\psi_{\rm ZN}\) [Eqs.(2.15) and (2.46)], \(\sigma_{\rm ZN}\) [Eqs.(2.15), (2.50) and (2.52)] and \(\delta_{\rm ZN}\) [Eqs.(2.25), (2.51) and (2.53)]
- NT.f computes the quantities in Sections 2.1.2 and 2.2.2 on pages 8-9 and 11-12.
- the transition probability, \(P_{\rm 12}\) [Eqs.(2.27), (2.54) and (2.59)]
- the phases, \(\bar{\phi_{S}}\) [Eq.(2.29)], \(\phi\) [Eq.(2.67)], \(\sigma_{\rm ZN}\) [Eqs.(2.28), (2.69) and (2.62)], \(\delta_{\rm ZN}\) [Eqs.(2.32), (2.70) and (2.61)], \(\Delta_{12, 11, 22}\) [Eqs.(2.36), (2.37), (2.38), (2.64) and (2.71)] and \(U_{1, 2}\) [Eqs.(2.40), (2.35) and (2.66)]
Note that the main subroutine (hop.f) returns the only hopping probability in the argument of "prob", but the phases listed above are shown on standard output (stdout) in computer (The default destination of stdout is the display screen on computer.). If the phases are required to be stored in arrays, users need to improve the arguments in "hop.f", "LZ.f" and "NT.f."
A. The interface of the main subroutine "hop.f"
Cartesian coordinates are employed for these arguments; the input/output is indicated in parentheses.
- etot1d: energy for hopping direction. (input)
- ek1d: kinetic energy for hopping direction. (input)
- v1d: velocity in the hopping direction. (input)
- dir: hopping direction. (input)
- r: current coordinate in atomic unit a_0. (input)
- v: current velocity. (input)
- ead: adiabatic potential energies in lower and upper potentials E_h. (input)
- prob: nonadiabatic transition probability. (output)
- natom: number of atoms. (input)
- nsurf: number of potential energy surfaces taken into account. (input)
- is0: index of the relevant state. (input)
- is1: index of the adjacent state. (input)
- keyhop: type for LZ transition \((E\ge E_X\ {\rm or}\ E\lt E_X)\) and NT transition \((E\ge E_b, E_b\gt E\ge E_t\ {\rm or} E\lt E_t)\) by 1-2 and 3-5. (output)
- kavail: flag indicating whether the transition is classically allowed or not. If kavail=1, etot1d is not enough to hop vertically. (output)
The sizes of dimension of the arguments are as follows;
- dir, r and v arrays are
\(\rm 3(x-, y-\ and\ z-components) \times matom; natom \leq matom\).
(matom is the maximum counting number of atoms defined in the including file, "para.inc.") - ead array is \(\rm msurf; nsurf \leq msurf\).
(msurf is the maximum counting number of potential surfaces defined in "para.inc.") - otherwise, all arrays are single values
B. The interface of the user-supplied subroutine "run_molpro.f"
Cartesian coordinates are employed for the arguments; the input/output is indicated in parentheses. This routine controls the ab initio calculation with the argument of "indgna" by 0, 1 and 2.
- r_c: current coordinates a_0. (input)
- v_c: adiabatic potential energy E_h. (output)
- dvdx_c: adiabatic potential energy gradient. (output)
- nacme_c: nonadiabatic coupling element (nonadiabatic vector). (output)
- tdm_c: transition dipole moment. (output)
- natom: number of atoms. (input)
- nsurf: number of potential energy surfaces taken into account. (input)
- isurf1: index of the relevant state. (input)
- isurf2: index of the adjacent state. (input)
- indgna controls the output of energy, gradients, non-adiabatic couplings and so on. (input)
- When indgna = 0, only the potential energy is stored in v_c.
- When indgna = 1, potential energy and its gradient are store in v_c and dvdx_c.
- When indgna = 2, potential energy and nonadiabatic coupling elements are stored in v_c and nacme_c
The sizes of dimension for the arguments are as follows;
- r_c, dvdx_c, nacme_c and tdm_c arrays are \(\rm 3 \times matom; natom \leq matom\). (matom defined in the including file, "para.inc.")
- v_c array is \(\rm msurf; nsurf \leq msurf\). (msurf defined in "para.inc.")
- otherwise, all arrays are single values
References
- [Original paper] Toshimasa Ishida Shinkoh Nanbu, and Hiroki Nakamura
Clarification of Nonadiabatic Chemical Dynamics
by the Zhu-Nakamura Theory of Nonadiabatic Transition:
From Tri-atomic Systems to Reactions in Solutions,
International Review in Physical Chemistry, X, XXXX-XXXX (2017)
DOI:10.1080/0144235X.2017.1293399
-> Draft Version - [Molpro12] H.-J. Werner et al., MOLPRO Version 2012.1; A Package of ab initio Programs, Cardiff University, Cardiff, UK, 2012.