統計力学II （担当　後藤） 　戻る （TOPページ)

【2008年度】

• 10/3統計力学II講義スタート。スピン共鳴も履修して欲しい、、、残念ながらほとんど履修してくれませんでしたので二年生にスピン演算子の講義をしてしまうハメになりました。

• 今年も一次元イジングの伝送行列をやりました。ランダウの現象論はやりませんでした。分子場は演習で吉澤先生がやってくれたそうなので説明だけにしました。伝送行列に入る前に、相転移の話を説明して、「自由エネルギーの交差の仕方から、潜熱が出るのが一次で、比熱に異常が出るのが二次転移」と仕込んでおいて、比熱を求め、異常がないので、相転移は無い、と結論し、大変なだけな磁化の計算は省略しました。すっきりまとまったと思います。

• 1/30無事でなく試験終了。朝、「来てやったぜ」「解答用紙です」「そんなもんいらん、自分で準備した」「でも名簿もお持ちいただかないと」「そんなもん注文しとらん。大体LOYOLAで作れるだろう」「お待ちを！」「うるさい。迷惑だ！」、、、、、試験終了後、昼頃に電話ルルルル 「後藤先生、○○長がお呼びです」「,,,@_@)；；；；；；」またやっちまったぜ。
  試験問題及び略解（2008年度)　
  

• フォトンと言っているのに、mやμの入った式をいじり倒したり、分散関係にE〜k²を仮定したりしてコケた人が多かったです。
  でも、「状態密度は分散関係と次元で決まる」と何回も言いましたよね。もっとも、「エネルギー密度を求めよ」と言いつつ、
  D(ε)f(ε)を計算させてしまった私も文句の言える立場ではありません、、。一人だけそのことを指摘してくれた人がいました。

【2007年度】

• 講義回数が増えたので、「伝送行列」まで行きました。厳密解を出すのがいかに
  大変か、そして分子場近似がたまに間違った答えを出すことがあるのがわかったと思います。

• 分子場とランダウの現象論（融解と超伝導）は「低温技術」の選択科目講義で説明しました。

• 出席率が非常に悪い（皆さん、講義の半ばにやって来ます）のが大変残念でした。orz

• 〔予想試験範囲〕S=1/2を5題（異なる次元を含む）、S=0を3題（三次元）。配点は6:4くらい。

• 配布プリント１、２、３、４、５、６、７、８、９、10 

• 試験問題・略解 （６９名受講、６６名受験、３名欠席）

  フォトンライクな分散を持つ一次元粒子を出題しました。D(ε)が定数になるので

  簡単に解けるはずなのですが、「状態密度は分散と次元に依存する」という基本的な
  ことを理解していないとハマッてしまう問題でした。
  
  

  　

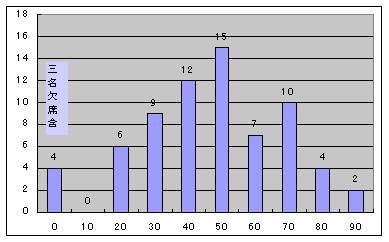
• 再履修は12名（うち欠席３名）、追レポートは15名です（提出締切は3月10日）。

【2006年度】

• 復活しました。計算が複雑なところはプリントにして配布しました。

• 計算が簡単なところは、学生さんが前に出てチャレンジしました。

• 【2006年度】試験問題、2005/01/26終了、（受験者54名）

  2006年度統計力学II試験結果　（担当　後藤）

  

  試験問題及び略解（2006年度)　　　　　　戻る

【前回の終了談】
講義担当(2001-2004)は終了しました。思えば苦しいながらも楽しい4年間でした。
まとめ (いずれ、「sma4winで学ぶ統計力学」とかをまとめたいものです)。
来年度(2005)はサバティカルです(後期のみ)。

• 計算が複雑なところはプリントにして配布しています(最新版を講義で配布)。

• 【2004年度】試験問題、　2005/01/14終了、（受験者47名）

• 【2003年度】試験問題、　2004/01/09終了、（受験者96名）
  

• 【2002年度】試験問題、　2003/01/10終了、合格者47名掲示（受験者59名）

• 【2001年度】試験は二回行いました。

０ スケジュール (括弧内は2004, 2003, 2002年度の進度）

１ 統計力学の目的　10/6, (10/1-10/8, 10/3, 9/27)

  1-1 量子力学と統計力学の関係(T=0とT>0)、統計力学と熱力学との橋渡し（F=-k_BTlogZ）

  1-2 ミクロカノニカル集合、カノニカル集合、グランドカノニカル集合、その他の集合

  1-3 ラグランジュの未定定数法による「状態」の実現確率の導出

２ 大分配関数 10/13, (10/15, 10/10, 10/4)

  2-1量子力学による粒子の統計性(ボース粒子、フェルミ粒子) 古典粒子との違い

　２-２ 粒子数表示、大分配関数、フェルミ分布関数（平均粒子数）

３ ボース分布とフェルミ分布  10/22-10/29, (10/17, 10/11)

　3-1 化学ポテンシャルとは。ボース粒子の化学ポテンシャルは常に負。

　３-２ ボース粒子と古典粒子の違い─どうしてボース粒子は古典粒子よりも密集しやすいか

４ 状態密度 10/20, (11/5, 10/24, 10/18)

  4-1 状態密度とは：変数変換の変換因子のようなもの、
　　　　     エネルギーの縮退の度合いのようなもの、状態の個数のヒストグラムのようなもの。

  4-2 箱に閉じ込められた自由なフェルミ粒子の絶対零度での性質
　　　　　　 化学ポテンシャルと圧力の計算

５ 有限温度におけるフェルミ粒子の性質 I   11/10, (11/12, 10/31ソフィア祭休講のため11/07,  10/25)

   5-1 ゾンマーフェルトの公式の導出

６ 有限温度におけるフェルミ粒子の性質 II  11/17, (11/19-26,  11/14, 11/1ソフィア祭休講のため11/8)

   6-１ 粒子数と化学ポテンシャル、エネルギーと比熱

   6-２ フェルミ粒子のヘルムホルツの自由エネルギーとエントロピーを大分配関数から求める

７ 磁場がかかった時の振る舞い  11/24(RAL帰国翌日), (12/3は創立記念日休講で12/10, 11/21, 11/15）

　７-１ 磁場、磁束密度、磁化、磁化率、帯磁率とは何か

　７-２ パウリ磁化とキュリー磁化

　７-３ 量子効果はどのようなときに現れるか(粒子の波動関数の重なり）

８ ボース粒子  I   12/1胃腸炎で休講12/8, (12/16補講, 11/28, 11/22)

　8-1 ボーズ統計、ボーズ分布

　８-２ 古典統計とボース粒子の違い（なぜ集まりやすいか）

　８-３ 自由なボーズ粒子のボースアインシュタイン凝縮

９ ボース粒子 II   12/15(前回の分とまとめて講義), (12/17, 12/05, 11/29)

　9-1 箱の中の自由粒子のボースアインシュタイン凝縮

　９-２ 調和ポテンシャル中の粒子のボースアインシュタイン凝縮 （レーザーによるドップラ冷却）

　９-３ 古典統計での調和振動子との違い
 

10 ボース粒子 III  12/22, (12/17, 12/12, 12/06)  

　10-0 超流動とBECの関係、ランダウ条件、フェルミ球からの励起の分散 【暴走しました】

　10-１ 光子（電磁波）、プランク分布

　10-２ 恒星の色─ウィーンの偏移則、ステファンボルツマンの法則

　10-３ 粒子もどきのボース統計 （固体中の格子振動などを「粒子もどき」とみなす）

　10-４ 固体の比熱（デバイモデル）

11 相互作用のある系   1/12, (12/19, 12/13)

　11-1 相互作用の無い系では一体問題と同じになること

　１１-２ 相互作用する二つのスピンの系、三つ、四つ...

　１１-３ 分子場近似（平均場近似）

※2004年度は補講をしてここまで来ました ［1/14試験］

 １２ まとめ、統計力学のあらすじ (12/20)
　１２-１ 八種類のアンサンブル
　１２-２ ミクロカノニカル、カノニカル、グランドカノニカル

　１２-３ 古典統計と量子統計、状態密度(2006年度も補講でやる予定でしたが日程が合わず中止)

※2002年度はここで終了しました［1/10試験］
 

１３　相互作用のある系 01/07(補講), （2003, 2001年度）

　１２-１ 相互作用する多くのスピンの系

　１２-２ 一次元イジングモデルの伝送行列による厳密解(2001年度のみで撤退)

※2007年度は伝送行列をやって、現象論や分子場、まとめは省略しました。［2/1試験］

※2008年度は相転移と伝送行列をやって、現象論や分子場、まとめは省略しました。［1/30試験］
 

14 相転移 （2006年度1/14,..., 2001年度）

　１３-１ 一次相転移と二次相転移、秩序変数

　１３-２ ランダウの現象論、過冷却と過加熱、潜熱

※2006年度はここまで行きました(伝送行列は不扱) ［1/26試験］
※2003年度は補講をしてここまで行きました(13,14は概略のみ、伝送行列は不扱) ［1/9試験］
※2001年度は補講をしてここまで行きました［試験は二準位系について］

<<<戻る　　　<<<TOP