Materials
Life
Environment
Analysis of the Ultraviolet Absorption Cross Sections
of Six Isotopomers of Nitrous Oxide (N2O)
using 3D Wavepacket Propagation
The loss of nitrous oxide from the atmosphere is very simple, involving photolysis in the stratospheric UV windows (90%);
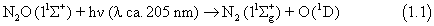
In 1997 Yung and Miller presented the "zero point energy" model,1 which revised our understanding of the role of photolysis in fractionating isotopomers. In this model the position of the absorption band of an isotopically substituted species is taken to be that of the main species shifted by the change in vibrational zero point energy. The ZPE model incorporates the invariance of the potential energy surfaces to isotopic substitution (Born-Oppenheimer approximation), and concludes that since the excited state is repulsive, increasing the vertical excitation energy by the ZPE change can approximate the isotope effect. Such a small shift of the band position would result in a significantly slower photolysis rate for heavy isotopomers, removing the imbalance in the isotopic budget and the need for exotic in situ sources. On the other hand, subsequent experiments showed isotopic enrichments about twice those predicted by the ZPE model, although qualitative agreement was observed.2
In the present work, the ultraviolet absorption cross sections of six nitrous oxide isotopomers (14N14N16O, 14N14N17O, 14N14N18O, 14N15N16O, 15N14N16O, and 15N15N16O) were computed using the wave packet propagation technique to explore the influence of excited state dynamics, transition dipole surface and initial vibrational state. The wave packet propagation technique used here was the "real wave packet" method .3 The wave packet is represented using evenly spaced Fourier grids for R and r coordinates, and a associated Legendre polynominals based discrete variable representation (DVR) for the angle θ in Jacobi coordinates. The absorption potential used in the real wave packet propagation is taken as
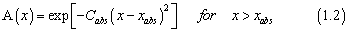
where x =R , xabs= 7.0 a0, and Cabs= 0.25, and where x =r , xabs= 6.0 a0, and Cabs= 0.25. To simulate the dissociation process induced by the photoexcitation, one must determine the initial wave packet correctly. In the time-dependent formulation, the product of the transition dipole moment function with the initial vibrational function of the electronic ground state gives the initial wave function.
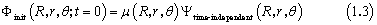
where μ(R ,r,θ) is the transition dipole moment function for the corresponding electronic transition, and Ψtime-independent (R ,r,θ) is the initial vibrational wave function of the electronic ground state. The resulting wave function Φinit (R ,r,θ; t = 0) is propagated on the potential energy surface (PES) of the electronically excited state. Therefore, we have calculated the vibrational wave functions of the ground state using the Hamiltonian matrix similar to that of the wave packet propagation; the PES was switched with that of the excited state and the implicitly restarted Lanczos method in ARPACK4 was used to diagonalize the matrix. After determining the initial wave packet, it was evolved with time on the PES of the electronic excited state, and finally the autocorrelation function was computed by numerically integrating the product of the initial wave packet and the evolving wave packet at each time step. Total photo-dissociation cross section as a function of the excitation energy was computed as the Fourier transform of the autocorrelation function as a function of time.
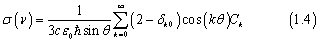
where Ck is the order-dependent autocorrelation function in the Chebyshev order domain. In the present work, photodissociation cross sections were computed assuming the total angular momentum J = 0 and 1.
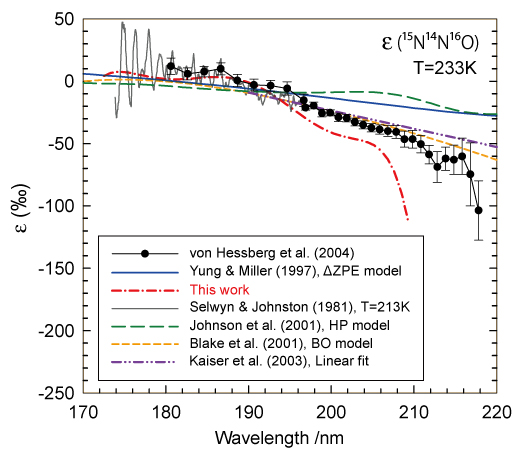
Figure 1. Fractionation constants for 15N14N16O isotopomer.
Numerous wave packet simulations were carried out and used to calculate the temperature-dependent photodissociation cross sections of the six isotopomers. The photolytic isotopic fractionation constants determined using the calculated cross sections are in good agreement with recent experiments (see Figure 1).
- [1] Y. L. Yung, C. E. Miller, Science 278, 1778 (1997).
- [2] P. von Hessberg, J. Kaiser, M. B. Enghoff,C. A. McLinden, S. L. Sorensen, T. Röckmann, M. S. Johnson, Atmos. Chem. Phys. Discuss. 4, 2333 (2004).
- [3] S. K. Gray, G. G. Balint-Kurti, J. Chem. Phys. 108, 950 (1998).
- [4] ARPACK [homepage] is a collection of FORTRAN 77 subroutines designed to solve large eigenvalue problems written by R. B. Lehoucq, K. Maschhoff, D. C. Sorensen, C. Yang, Rice University (Houston), 1997.