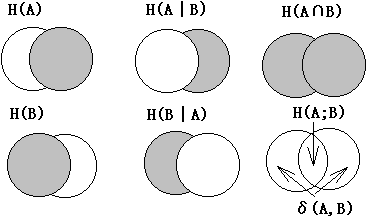田中裕

【Ｉ】 べルの不等式の破綻と非古典論的世界の現実性

（I）歴史的背景：ＥＰＲ論文とベルの定理の連関

（Ａ）ＥＰＲの議論の前提

（１）物理量の実在性を判定する基準（十分条件）（２）物理理論の完全性を判定する基準（必要条件）（３）量子力学に基づく統計的予測の経験的な正しさ

（Ｂ）ＥＰＲの議論の形式的構造：

命題Ｃ（Completeness)：量子力学（波動関数による実在の記述）は完全である．

命題Ｓ(Simultaneous Reality)：相補的な（交換しない作用素で記述される）物理量が同時に実在性をもつ．

命題Ｌ（Locality)：空間的に十分に隔てられた二つの場所
（ｃ^2ｄｔ^2−ｄｌ^2＜０)でなされる観測（観測装置／対象の選択）は因果的に独立であって，測定結果に影響しない．

ＥＰＲ論文の著者自身による量子力学の 命題Ｌを前提として明示したＥＰＲ

不完全性の論証の形式的構造 の論証の再定式化

大前提（不確定性原理）：〜Ｃ ∪〜Ｓ 大前提： 〜Ｃ∪ 〜Ｓ 

小前提（EPRの思考実験）： Ｃ→Ｓ 　　小前提： Ｃ ∩ Ｌ→Ｓ

　　　　　　　　　　結論： 〜Ｃ 　　　結論： 　Ｌ→ 〜Ｃ 

ＥＰＲの議論とベルの定理との関係

ＥＰＲの議論の結論（局所性を前提すれば量子力学は不完全である）: Ｌ→ 〜Ｃ

ベルの定理（局所的隠れた変数の理論は量子力学と矛盾する）：〜 (Ｌ∩ 〜Ｃ）

　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　結論 ： 〜Ｌ 

（Ｃ）ＥＰＲの議論とベルの定理の両方を受け入れるならば，局所性の前提Ｌは放棄しなければならない．しかしながら、局所性の原理の破綻が、遠隔作用の実在性を意味するのであれば、量子力学と相対性理論との整合性の問題が改めて生じる．一部の論者は、相対性理論を、「ローレンツ以前の状況」に戻して、絶対時間と絶対空間の概念を復活させる試みに着手しているので、我々は、このような試みが果たして妥当なものであるのかどうか、また、量子論的な「非局所性」とは、いかなる性質のものであるのか、という問題を次に考察しよう。

【２】Ｌの放棄と相対性理論との整合性

（１） ＥＰＲ（量子論的遠距離）相関は，非決定論的な偶然的事象系列のあいだに成り立つ相関関係であって，一方の事象系列を実験的に操作することによって，超光速度の遠距離通信に利用することはできない（操作不可能な非局所性）.それゆえＥＰＲ相関は，エネルギーや信号を瞬間的に遠方に伝達するという意味での遠隔作用ではないから，相対性理論の潜在的反証者（potential falsifier)を現実化したものではない．

（２）ＥＰＲ相関そのものは，相関する二項のあいだの絶対的な時間的順序については何も語らないから，時間的継起に絶対的順序があることを証明しない．したがって，相対性理論にかわって絶対基準系を前提するローレンツ理論をなんらかの形で復活させるのは適当でない．ＥＰＲ相関は『隠れた変数の理論』によらずに，またエーテルのような『隠れた実在』や『遠隔作用』ぬきで説明されねばならない．

（３）量子力学においては、「分離不可能な実在」という概念によって、観測者を含む全体を解釈する一般的な理論枠組が必要である。我々は、素朴な実在論の立場をとることは許されず、観測される前の物理系の状態が、すべての点において、観測者である我々とは独立に実在すると前提することは出来ないからである。しかしながら、それと同時に、量子力学は全面的な反実在論をとるものでもないことにも留意しなければならない。電子のスピンが１／２であること、その質量が一定の値をとることなどについては、量子力学もまた、実在論の立場で語っているからである。

【３】分割不可能な実在： 量子論の要求する実在概念

（１）客観と主観：量子論における対象系は，観測者に対するパースペクティブを抜きにしては定義することができない．したがって観測されるものと観測するものを分離することはできない．

（２）全体における部分：量子論的システムのある部分の記述を他の部分の記述から分離することはできない．そこにおいては部分の記述よりも全体の記述が優先する．

（３）可能性と現実性：量子論的システムに現れる非決定論は確率の主観的解釈（外界に対する我々の知識の不足）と隠された因果的なメカニズムの想定によっては説明されない．それは確率の客観的解釈（潜在的可能性の尺度）を必要とする．この非決定論は，全面的な非決定論ではなく，それぞれが偶然的である二つの事象のあいだに，決定論的な遠距離相関を許容するという意味で，独自のものである．

（４）過去の経歴の不確定性：不確定性原理は，未来に対してだけでなく系の過去の経歴にも適用されねばならない（遅延選択実験）．古典論的世界においては、過去の経歴は観測者抜きでただ一つに確定しているが、量子論では、観測される系の過去の可能な経歴のすべてが現在の測定結果にかかわりを持つ（経歴総和法）.それは，現在の観測が過去の「事実」に影響を与えるという意味での、逆向きの因果を認めることではなく，過去の歴史が観測されなくともすべて確定しているという古典論的前提を放棄すべきことを我々に要求する．相対性理論が４次元時空で存在する（永遠の相における）事象を記述するとすれば，量子論は４次元時空で非局所的に生起する事象という新しい概念を必要とする．

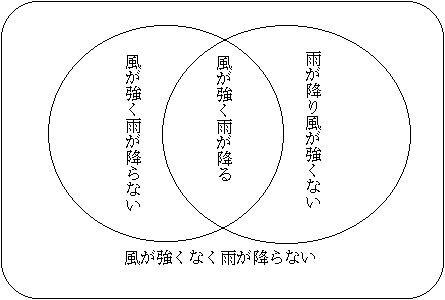
【４】古典論的世界とベルの不等式

−分割不可能性の量子論理的側面−

ここでは、事象の分割化の可能性ということを定義し、それが論理法則を経験的世界に適用する際に、我々が暗黙の内に前提していたことを明るみに出し、この前提が量子力学では、無条件では成立しないことを示そう。これは、量子論理へ「自然な」導入となるべきものである。

　　次の二つの経験的事象を考えよう。

ａ：明日は風が強い。ｂ：明日は雨が降る。

この二つの事象は、いずれも明日の天気について語る文によって記述されている。一般に、事象は命題と異なり、真か偽かという二値をとるのではなく、多値的な確率を付与して語られることに注意しよう。確率論の教科書では、命題と事象を区別しないものも多いが、ここでは、命題とは、我々がその真偽を知る知らぬに関わらず、真偽の確定しているものを指すことにする。そうすれば、ａやｂのような文で記述される事態を命題と呼ぶときには、我々は、明日の天気は今日すでに確定していると言わなければならないだろう。しかし、確率論が主題とする世界は、このようにすべてがあらかじめ決定されているような世界ではない。

　それ故に、命題(proposition)と事象（event)を区別するほうが、我々の主題が決定論を前提しないという主旨を明確にするであろうし、事象という用語を使うならば、確率論を、ａやｂのような状況依存的な指示詞（明日）を含む文にも適用できるわけである。そして、命題と事象の区別を明確にすることは、我々の主題である量子論理の性格を理解するうえできわめて重要であるのも関わらず、従来、この点が看過されてきたように思われる。実際、三値以上の真理値を持つ「命題」論理として量子論理を体系化したり、あるいは、真理値を前提しない純粋に形式的な議論においても、古典論理の基本法則である分配法則が成り立たない「命題」論理として量子論理を体系化するといったことがふつうに行われている。しかしながら、後で示すように、偶然性を排除している古典論理の世界で意味を持つ「命題」という概念は、量子論理では狭すぎるのである。そこで、まずはじめに、量子論理が第一義的に関わりを持つのは、「事象」であって、「命題」ではないということを明確にしておこう。

　　さて、二つの事象ａとｂについて、ａがｂによって分割可能（divisible)であることを ａＤｂで表し、次のように定義しよう。

（1）　ａＤｂ ←→ def ａ＝（ａ∩ｂ）∪（ａ∩¬ｂ）

　この定義式の右辺は、日常的にはアプリオリに前提されている等値関係であるといって良いであろう。「明日は風が強い」ということは、「明日は風が強く雨が降るか、または、明日は風が強く雨がふらないか、いずれかである」と等値である。それは、明日の天候について語るときに、様々な述語によって、場合分けするときに、我々がほとんど無意識のうちに前提している。この等値関係は、次のようなベン図を使うことによって、最も明確に示されるだろう。

このような図示が可能であるということは、

ここでの定義に従えば、「雨が降る」という述語によって規定された明日の天気に関する事象ａが、「風が強い」という述語によって規定された明日の天気に関する事象ｂによって、分割可能であることを意味しているのである。そして、ベン図が示していることは、ａがｂによって分割可能であるばかりでなく、ｂもａによって分割可能であること、さらには、事象ａ、¬ａ、及び、ｂ，¬ｂという四つのうち、どの二つをとっても相互に分割可能であるということである。

そこで、二つの事象ａとｂとが相互に分割可能であるとき、「ａとｂとは通約可能(commensurable)である」と呼び、ａＣｂで表すこととしよう。

（２） ａＣｂ ←→ def ａＤｂ＆ｂＤａ

我々の目的は、分割可能性ないし通約可能性の概念によって古典論的世界を特徴づけることである。

ここで、古典論的世界という時、それは古典的な命題論理によって我々によってモデル化された事象の集合としての「世界」を意味している。それは、例えば ヴィトゲンシュタインが「論理哲学論考(Tractatus)」において「世界」という語を使用したときは、それは「物の集まりではなくて、事象(Tatsache)の集まり」を意味していた。「物の世界」がその構成要素（分子や原子）に還元され再構成されるのと同じように、「事象の世界」もより原子的な事象に分割されることによって再構成されるのである。さて、物理学に於ける原子論が、必ずしももはやそれ以上分割できない絶対的な原子の存在を前提する必要がないのと同じく、複合的な事象を要素的な事象に分割してその総和として再構成できるという事を認める理論は、事象の原子論といってよいであろう。そこでは、原子的事象は、事象を記述する我々の言語にたいして、相対的に定まるものであってもかまわないのである。

　世界という語を上のような意味に解して、古典論的世界を、そこにおいては、あらゆる事象が通約可能であるような世界として特徴づけよう。

（３） 世界 Ｗc が古典論的である←→def " ａ，ｂεＷc ： ａＣｂ

　この様な、すべての事象が相互に通約可能である世界においては、「世界の完全な記述」という概念に、次のような意味を与えることができる。まず、論理的スペクトルという予備的概念を定義しよう。

　　相互に排他的であってかつ網羅的（ｉ≠ｊならｂi∩ｂj＝０ 　）な事象の集合 Ｂ＝｛ｂk｝を論理的スペクトルと呼ぶことにする。古典論的世界においては、どの事象ａも，論理的スペクトルＢによって の様に直和分解される．

のように直和分解される．

論理的スペクトルの概念によって，我々は，『古典論的世界の完全な記述』という『理念』を次のように定義できる．

とおけば，任意の事象ａに対して， ａÇ ｗm＝０かまたはａÇ ｗm＝ｗm となることである．このとき任意の事象ａは ｗm の直和に分割される．それぞれのｗm が世界の可能な完全記述に対応している．

古典論的世界においては，すべての事象に対して，それが生起する先験的確率を定義できる．たとえば，原子的な事象は先験的に等確率であると仮定すれば，原子的事象の総数をＮとして，a Ç ｗm＝ｗm となる ｍ（ａ）の総数をｎとして

となる．

この確率が，古典的な確率論の公理を満たすことは明らかである．一般には，

が成り立つ．

　　一般にニュートン物理学やそれに基づく統計力学では、この様な古典的な確率論の計算方法が前提されており、それらは、いずれも事象の分割可能性を認める原子論の上に成り立っていたといえる。原子事象と複合事象との関係は、命題論理の言葉で言い表せば、真理値関数の関係であって、原子命題の真理値がすべて決まれば、複合命題の真理値はそれによって決定されるという意味で、複合事象はその構成要素となる原子事象を指定することによって完全に記述されるのである。

　　さて、量子力学においては、ここで前提されていたような古典論的な世界の枠組みに収まらない事象が存在する。そこでは、事象の分割可能性が必ずしも成り立つとは限らないのである。一見して自明に見える公式（１）が成立しない理由は何であろうか。それは、量子力学の相補性解釈を提示したＮ．ボーアが、量子論的事象の「一体不可分性ないし個体性(individuality) 」と呼んだものと深い関わりを持っているのである。

　　量子力学の解釈をめぐる論争の中で、特に有名なものは、前節で分析したアインシュタイン・ボーア論争であるが、世界の完全な記述という概念を量子論理の立場から批判すれば次のようになるだろう。

　最も簡単な量子力学的事象の例として、電子のスピン成分を考えてみよう。

ａ：電子はｘ方向にスピン＋１をもつ． ｂ：電子はｙ方向にスピン＋１をもつ．

¬ｂ：電子はｙ方向にスピンー１をもつ

　　量子力学において異なる方向のスピン成分は可換ではないから、 事象ａを事象ｂによって分割することはできない．すなわち，『電子はｘ方向にスピン＋１をもつ』という事象を，さらに細かく分割して，『電子はｘ方向にスピン＋１をもちｙ方向にスピン＋１をもつか，またはｘ方向にスピン＋１をもちｙ方向にスピンー１をもつかいずれかである』というように二つの事象の直和に分割することはできない．

　　ここで注意すべき事は、分割不可能性ないし個体性の意味は、如何なる事象によっても分割できないという意味ではなく、それによって分割できないような事象があるということを意味する事である。例えば、電子が特定の方向に＋１のスピン成分を持つという事象と、電子がかくしかじかの位置にあるという事象とは通約可能（相互に分割可能）である。それゆえに、ある事象が個体性を持つことを次のように定義するのが妥当だろう。

（４）事象ａは個体性をもつ←→def （$ ｘ)(〜ａＤｘ）

　　個体性を持つ事象が存在すれば、それを分割できない事象があるということであるから、古典的な確率計算のアルゴリズムは当然制約を受けることになる。事象ａの生起する確率ｐ（ａ）を，ａと通約不可能な事象ｂによって分割して、二つの原子的事象 ａ∩ｂと　の生起する確率の和として表現することができないということを意味しているのである。即ち、自明に見える式、　　の成立を主張することができないのである。

　　我々は、この様な量子力学独特の事情を、古典論的な世界に収まらぬ事象を量子力学が含むという形で表現するために、次のように、量子論的世界を定義することにする。

（５）量子論的世界とは，分割可能性の関係が対称的であるが，通約不可能な事象が存在する世界である．

　　束論の用語を使えば，古典論的世界はブール束であるが，

量子論的世界はオルトモジュラー束である．

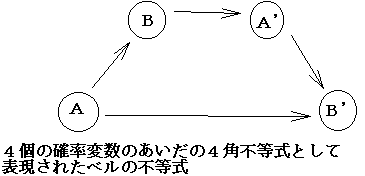
（Ｃ）古典論的世界における情報理論の定理としてのベルの不等式の定式化：

ＡとＢとを観測可能な量（observable)とする。情報理論によれば、Ａを測定してａi Ｂを測定してｂj が得られたときに新たに獲得された情報量は，

Ｉ（ａi）＝−ｌｏｇｐ（ａi），Ｉ（ｂj）＝−ｌｏｇｐ（ｂj），両者を合計した結合情報は，Ｉ（ａiÇ ｂj）＝−ｌｏｇｐ（ａiÇ ｂj）同様にして，

Ｉ（ａi｜ｂj）＝−ｌｏｇｐ（ａi｜ｂj） はＢの値ｂjが既に知られているという条件のもとで Ａの値ａiが知られたときに追加された情報を表す。ベーズの定理より、

Ｉ（ａiÇ ｂj）＝Ｉ（ａi｜ｂj）＋Ｉ（ｂj）＝Ｉ（ｂj｜ａi）＋Ｉ（ａi）

ＡとＢの様々な値が知られたときに獲得される情報の平均値（期待値）は

Ｈ（Ａ）＝ Σiｐ（ａi）Ｉ（ａi），　Ｈ（Ｂ）＝ Σjｐ（ｂj）Ｉ（ｂj）

ＡとＢの結合情報の平均値をＨ（ＡÇ Ｂ）で表示すると，

Ｈ（ＡÇ Ｂ）＝ Σi,jｐ（ａiÇ ｂj）Ｉ（ａiÇ ｂj） また

Ｈ（Ａ｜ｂj）＝ Σiｐ（ａi｜ｂj）Ｉ（ａi｜ｂj）はＢの値ｂjが与えられたときＡによって担われる情報である。Ｈ（Ａ｜ｂj）を更にＢについて平均すれば，

Ｈ（Ａ｜Ｂ）＝ Σjｐ(ｂj)Ｈ(Ａ｜ｂj)＝ Σi,jｐ(ａiÇ ｂj)Ｉ(ａi|ｂj)

ベーズの定理の直接的結果は

Ｈ（ＡÇ Ｂ）＝Ｈ（Ａ｜Ｂ）＋Ｈ（Ｂ）＝Ｈ（Ｂ｜Ａ）＋Ｈ（Ａ） である。

われわれはもう一つの情報，すなわち，相関情報を次の様に定義する。

Ｉ（ａi；ｂj）＝Ｉ（ａi）−Ｉ（ａi｜ｂj）＝Ｉ（ｂj）−Ｉ（ｂj｜ａi） この相関情報は正にも負にもなり得るが、その平均値は負にはならない。

Ｈ（Ａ；Ｂ）＝ Σi,jｐ(ａiÇ ｂj)Ｉ(ａi；ｂj)

＝ Σjｐ(ｂj)(Σiｐ(ａi|ｂj)ｌｏｇ(ｐ(ａi|ｂj)/ｐ(ａi))) ≧０

（ギプスの定理による：この定理の証明については、渡辺慧「知識と推測」上２２頁参照）. それゆえに，基本的な不等式

☆Ｈ（Ａ｜Ｂ）≦Ｈ（Ａ）≦Ｈ（ＡÇ Ｂ） が成り立つ。左側の不等式は、条件を除去することはある観測可能量によって担われる情報量を決して減らさないということを意味し、右側の不等式は二つの観測可能量は、単独の観測可能量より少ない情報を担うことはないということを意味している。この不等式に基づいてベルの不等式を導出しよう。

二つの物理的に分離された系、αとβを考え、αには観測可能な量（オブザーバブル）ＡとＡ’が，βには観測可能な量ＢとＢ’とが結合しているとする。これらのオブザーバブルの（離散的な）可能な値を，ａi , ,,ａk’,ｂj ,ｂl 'で表示する。これらの四つのオブザーバブルの観測値が分割可能な実在に対応すると仮定すれば、

結合確率ｐ（ａi Ç ａk'Ç ｂj Ç ｂl'）が存在するから，前と同様の統計的考察を行うことができる。基本不等式☆の一般化は

◎Ｈ（ＡÇ Ｂ')≦Ｈ（ＡÇ ＢÇ Ａ'Ç Ｂ')＝Ｈ（Ａ｜ＢÇ Ａ'Ç Ｂ')＋Ｈ(Ｂ|Ａ'Ç Ｂ')

＋Ｈ(Ａ'|Ｂ')＋Ｈ(Ｂ')

この不等式の右辺は、分割可能性の成立しない量子論的世界では定義できない確率を含むが, 我々は☆の左側の不等式を一般化して、量子論的世界でも定義できる条件付き確率を含む式に変形することができる。

すなわち， Ｈ（Ａ｜ＢÇ Ａ'Ç Ｂ')≦Ｈ（Ａ｜Ｂ）, Ｈ(Ｂ|Ａ'Ç Ｂ')≦Ｈ（Ｂ｜Ａ'）

を利用し、更にＨ（Ｂ') を◎の両辺から引くことによって、我々は情報理論によって表現されたベルの不等式を得る。

この四つの条件付の情報は量子力学で定義される確率によって表現される．それらは実験の統計的データによって確定する。 情報の距離という概念を使って，このベルの不等式をＡ，Ｂについて対称的に表現することもできる．

情報距離の定義：δ（Ａ，Ｂ）＝Ｈ（Ａ｜Ｂ）＋Ｈ（Ｂ｜Ａ）

情報距離の概念を用いたベルの不等式は，次のような四角不等式である．

これは、おそらくもっとも一般的な形式で表現されたベルの不等式であろう。古典論的世界においては、この不等式は分析的な真理（必然的真理）である。したがって、ベルの不等式の不成立が実験によって見出されたことは、古典論的世界の枠組みのなかには収まらない現象が実在することを示したものと解釈することができよう。

付録

確率変数ＡとＢとのあいだの相互依存性と情報距離の図解

　δ(A,B')≦δ(A,B)＋δ(B,A')＋δ(A',B')