一酸化二窒素 (N2O) 同位体の光解離反応と同位体効果
大気において窒素分子 (N2) に次いで存在量が多い窒化物が一酸化二窒素 (N2O) である。 窒素分子は極端に不活性な気体であるが、一酸化二窒素はそれに比べると不安定な分子であり、生物地球化学的な窒素循環の中で中心的な役割を果たしている。 また近年特に話題に上っている「温室効果ガス」のうちの一つとされているが、大気中のN2O濃度は産業化以前と比べ約17%も増加している。 おまけに、成層圏におけるN2Oの酸化反応がオゾン層破壊の触媒となっていると言われている。
この大気中のN2Oは土壌や海洋中の微生物活動が主な発生源であり、農業で使われる肥料によってその発生が活性化される。 しかしながらこの発生があまりにも拡散的であるために、N2Oの排出量を見積もることは大変困難である。 そこで、大気中に含まれる同位体の分析を行いN2Oの総量を試算することになっている。 そのため、本来安定とされる同位体元素14N、15N、16O、17O、18Oを使った同位体分布の野外観測が至る所で行われている。 その中でも特に重要な同位体種として14N14N16O、14N15N16O、15N14N16O、15N15N16O、14N14N17O、14N14N18Oが挙げられる (以降、これらの同位体種を [446]、[456]、[546]、[556]、[447]、[448] とそれぞれ呼ぶことにする)。 N2Oの主な発生源である土壌及び海洋中のバクテリアは、対流圏の空気に比べて重い窒素や酸素の同位体を含んだN2Oを生成していることが知られる。
上記のように拡散量が不明であった一方、大気におけるN2Oの減少に関するメカニズムは大変明解であって、90%が成層圏の紫外線窓領域における光分解

であり、残り10%が O(1D) との反応である。 この光分解反応 (1.1) は、182nm付近に中心を持つ幅の広い吸収ピークに対応する、最初の電子吸収帯の低エネルギー側で起こる。 そこで同位体種 [446]、[456]、[546]、[556] に対し、185nmの光による光分解反応や173〜197nmの範囲における光吸収断面積の観測が行われた。 しかしながら、大気中のN2Oの総量を理解する上で重要であり最も基礎的な問題である「同位体濃縮現象」と結びつく手がかりは観測されなかった。 そのため、N2O同位体濃縮が起こる理由として、他の付加的な発生源が提案された。
ところが、1997年にYungとMillerにより提案されたΔZPEモデル1 によって、同位体分離における光解離の役割についての我々の理解は大きく変えられた。 彼らが提案したΔZPEモデルの要点は「同位体種間の零点振動エネルギー(zero point energy)の差異 (ΔZPE) により吸収の周波数帯がシフトする」というものである。 彼らはΔZPEモデルにおいて (1) 同位体に対してポテンシャルエネルギー曲面は不変であるとし (2) 励起状態が反発形のポテンシャルであることから、垂直励起エネルギーがZPEの差異により増加するので同位体効果が表れると説明した。 確かに大気における光分解反応 (1.1) は各同位体の吸収帯のピーク位置から離れた (裾野の) 周波数で起こっており、バンドのピークのちょっとしたエネルギー差異が、バンドの裾野にあたる周波数域において重い同位体種の光吸収断面積を減少させ、結果として光分解速度を十分に遅らせることとなっているという説明はリーズナブルである。 近年の観測結果によると、ΔZPEモデルが定性的には一致した結果を与えている一方で、ΔZPEモデルによって予想される同位体濃縮効果は実測の半分程度であることが示されている。2
そこで我々の研究室では、量子論に基づく反応動力学計算を行い、ΔZPEモデルによる同位体効果の期待値と最新の実験結果との間にある2倍の差異の原因を解明することを目的として、理論研究を行っている。 また、このようにN2Oは大気化学分野において大変重要な分子の一つである一方、素反応過程を研究する上でのベンチマーク的な系として基礎科学的な観点からも注目されていて、そこでは「光解離により生じるN2フラグメントの振動回転準位分布の決定」と「等原子価軌道を持つOCS (硫化カルボニル) の光解離過程との比較」が最近のホットトピックスとなっている。 つまり、反応途中に存在する非断熱遷移過程の影響がこの二つの系において同様に観測されるかどうかという問題に話題が集中しており、根本的には我々がこれまでも対象としてきた非断熱遷移現象の範疇でもある。
我々は最近、量子波束計算を行い、N2Oの6つの同位体種 [446]、[447]、[448]、[456]、[546]、[556] に対する紫外光吸収断面積を理論的に求めた。 今回、波束発展法には"実空間波束発展法"3を用いた。 その際、Jacobi座標 (内部座標) 系における座標R およびr に対しては正弦フーリエグリッド変換法 (井戸型ポテンシャル基底) を、角度θに対してはGauss-Legendre求積法を基とした完備関係式をグリッド表現に焼きなおしたDVR (discrete variable representation) 表現を用いている。 また、実空間波束発展法で用いた吸収ポテンシャル (absorption potential) は

のようにとった。ここでx =R のときxabs= 7.0 a0 およびCabs= 0.25 で、x =r のときxabs= 6.0 a0 およびCabs= 0.25である。
光励起に伴う解離過程を記述するには、初期波束を適切に決定する必要がある。 時間依存型の表式において、初期波動関数は電子基底状態の初期振動波動関数と遷移双極子との積

で与えられる。 上式において、μ(R ,r,θ) が対応する電子遷移の遷移双極子、Ψtime-independent (R ,r,θ) が電子基底状態の初期振動波動関数である。 本式で得られる初期波動関数 (初期波束) Φinit (R ,r,θ; t = 0) を電子励起状態のポテンシャルエネルギー面上で伝播させる訳である。 したがって、電子基底状態の振動波動関数と波束の伝播を計算する必要がある。 ARPACK4で利用可能なランチョス反復法 (implicitly restarted Lanczos method) を用いてハミルトン行列 (Hamiltonian matrix) の対角化を行った。
こうして得た適切な初期波束を電子励起状態のポテンシャルエネルギー面上で時間発展させ、最終的に各時刻の波束と初期波束との自己相関関数 (auto-correlation function) を求める。 この自己相関関数を時間領域とエネルギー領域の間でFourier変換すると光解離の全吸収断面積が求められる。

上式においてCk はChevyshev次数に依存する自己相関関数である。
我々はこれまでに前述の6つの同位体種に対して、全核運動量J = 0 および 1 の場合の吸収断面積を求めた。 図1に同位体種 [546] に対する同位体分別定数註1 を波長に対してプロットした図を示す。 YungとMillerのΔZPEモデルはvon Hessvergらによる最新の実験結果の半分程度の値を与えるのに対し、我々が行った量子波束計算は実測値を形状まで再現している (値が高波数側にシフトしているのは用いた初期波束が原因なのであるが、我々はab initio計算に基づいて議論を行うグループなのでscaling factorによる補正を行うつもりはない)。

図1. N2O同位体 [546] に対する同位体分別定数 (ε)。 縦軸の値は千分率 (‰)。
- [1] Y. L. Yung, C. E. Miller, Science 278, 1778 (1997).
- [2] P. von Hessberg, J. Kaiser, M. B. Enghoff,C. A. McLinden, S. L. Sorensen, T. Röckmann, M. S. Johnson, Atmos. Chem. Phys. Discuss. 4, 2333 (2004).
- [3] S. K. Gray, G. G. Balint-Kurti, J. Chem. Phys. 108, 950 (1998).
- [4] ARPACK [homepage] is a collection of FORTRAN 77 subroutines designed to solve large eigenvalue problems written by R. B. Lehoucq, K. Maschhoff, D. C. Sorensen, C. Yang, Rice University (Houston), 1997.
-
註1 同位体分別定数 (ε) は以下の式
で定義され、値が負に大きいほど重い同位体の光解離に対する
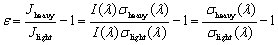
吸収断面積が小さいので、つまり、存在比が大きいことを表す
(強い同位体濃縮が起きていることを示す) 指標である。